Валидное Судоку

Средняя
medium , matrix , hash table
21 November 2023

Описание задачи #

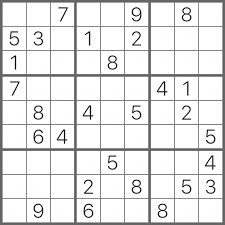
Судоку

Вам дана доска Судоку размером 9 x 9. Определите, является ли эта доска валидной. На валидность проверяются только заполненные ячейки в соответствии со следующими правилами.

  1. Каждая строка должна содержать цифры от 1 до 9 без повторений.
  2. Каждый столбец должен содержать цифры от 1 до 9 без повторений.
  3. Каждый из девяти квадратов доски размером 3 x 3 должен содержать цифры от 1 до 9 без повторения.

Доска Судоку (частично заполненная) может быть валидной, но не обязательно решаемой. Только заполненные ячейки должны быть проверены в соответствии с упомянутыми правилами.

Ограничения #

Примеры #

  • Входные данные

    [
    ["5","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"],
]

    Ответ: true

  • Входные данные

    [
    ["8","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"],
]

    Ответ: false

Решение #

В первую очередь, чтобы решить эту задачу, надо придумать каким образом отслеживать уникальность значений в каждой строке, столбце и квадрате. Для этого мы создадим несколько вспомогательных структур фиксированной длины для отслеживания используемых значений.

Самая сложная часть этой задачи заключается как раз в том, чтобы понять, как должны работать эти структуры.

Для начала определим квадратную матрицу (массив массивов) rows фиксированного размера. То есть в нашей матрице будет 9 строк по 9 колонок в каждой.

Как мы будем фиксировать наличие цифры в строке? Например, если в нулевой строке есть цифра 3, то мы установим значение true в rows[1][2] — в качестве индекса i используем индекс строки, а в качестве j значение цифры - 1. То есть нулевой индекс в нулевой строке фиксирует наличие цифры 1, первый индекс — цифры 2, второй индекс — цифры 3 и так далее. Точно такой же подход будем использовать для фиксирования наличия значений в столбцах, поэтому создадим матрицу columns размера 9 х 9.

С определением наличия одинаковых цифр в каждом квадрате дела обстоят немного сложнее, но не сильно. Сначала в уме индексируем каждый квадрат в матрице.

Судоку с индексами

Например, координата 1:1 в таком случае будет обозначать средний квадрат, а 2:2 — нижний правый. Теперь мы заведем Hash Map с названием quads для хранения сведений о встречающихся в квадрате цифрах. В качестве ключа мы будем использовать строку с координатой, а в качестве значения массив длиною в 9 элементов, такой же как в матрицах rows и columns. Таким образом если мы хотим указать, что в среднем квадрате, например, находится цифра 2, то нам нужно в мапу под ключом 1:1 создать массив и в этот массив под индексом 1 положить значение равное true.

После того как мы разобрались с этой частью алгоритм становится совсем простым.

Мы обходим все элементы матрицы и проверяем только те, где есть цифры. Если в матрицах rows, columns и в мапе quads для искомой цифры все значения равны false, значит эта цифра пока что уникальна. В таком случае устанавливаем все значения в true и переходим на следующую итерации.

Если же хоть в одной из структур будет значение равное true, то это означает что такая цифра уже существует и не является уникальной. В таком случае мы можем прервать функцию и вернуть ответ false.

Если же мы пройдем по всей матрице и ни разу не встретим значение true, то все элементы уникальны и из функции можно вернуть ответ true.

Кстати, для определения координаты квадрата нам достаточно индекс колонки и строки в матрице поделить на 3 без остатка.

  • package main

import (
	"fmt"
	"strconv"
)

func isValidSudoku(board [][]byte) bool {
	rows := [9][9]bool{}
	columns := [9][9]bool{}
	quads := make(map[string][9]bool, 9)

	n := len(board)

	for row := 0; row < n; row++ {
		for col := 0; col < n; col++ {
			if board[row][col] == '.' {
				continue
			}

			strNum := string(board[row][col])
			num, _ := strconv.Atoi(strNum)
			pos := num - 1

			key := fmt.Sprintf("%d:%d", row/3, col/3)

			if rows[row][pos] || columns[col][pos] || quads[key][pos] {
				return false
			}

			rows[row][pos] = true
			columns[col][pos] = true

			temp := quads[key]
			temp[pos] = true
			quads[key] = temp
		}
	}

	return true
}

  • export const isValidSudoku = (board: string[][]): boolean => {
    const n = board.length

    const rows: boolean[][] = []
    const columns: boolean[][] = []
    const quads: Record<string, boolean[]> = {}

    // Предварительно заполняем массивы false значениями
    for (let i = 0; i < n; i++) {
        rows.push(new Array(n).fill(false))
        columns.push(new Array(n).fill(false))
    }

    for (let row = 0; row < n; row++) {
        for (let col = 0; col < n; col++) {
            if (board[row][col] === '.') {
                continue
            }

            const pos = Number(board[row][col]) - 1
            const key = `${Math.floor(row / 3)}:${Math.floor(col / 3)}`

            if (!quads[key]) {
                quads[key] = new Array(n).fill(false)
            }

            if (rows[row][pos] || columns[col][pos] || quads[key][pos]) {
                return false
            }

            rows[row][pos] = true
            columns[col][pos] = true
            quads[key][pos] = true
        }
    }

    return true
}

Оценка сложности #

По времени

Так как мы перебираем всю матрицу, то сложность перебора будет равна O(n2).

По памяти

В сумме мы используем 3 * n2 дополнительной памяти, поэтому итоговая сложность равна O(n2).

Оригинал задачи на Leetcode
< Предыдущая задача
Следующая задача >