Произведение элементов массива исключая себя

Средняя

medium , array , prefix sum

28 November 2023

Описание задачи #

Вам дан целочисленный массив nums. Напишите функцию, возвращающую в качестве ответа такой массив, в котором на i-ой позиции будет число, равное произведению всех элементов массива nums, кроме i-го.

Дополнительно попробуйте решить задачу так, чтобы обеспечить линейную сложность O(1) по памяти. Выходной массив не считается за выделение дополнительной памяти.

Ограничения #

В массиве может быть от 2 до 10⁵ элементов
Значение каждого элемента находится в диапазоне от -30 до 30
Произведение любого префикса или суффикса чисел гарантированно вписывается в 32-битное целое число
Запрещено использовать операцию деления в реализации

Примеры #

Входные данные: [1,2,3,4]

Ответ: [24,12,8,6]
Входные данные: [-1,1,0,-3,3]

Ответ: [0,0,9,0,0]

Решение #

В этой задаче мы даже не будем пытаться разбирать брутфосрс решение, так как очевидно, что оно будет очень затратным. Тем более, что есть очень простое и интуитивно понятное решение за линейное время.

Произведение всех элементов массива кроме одного находится очень просто, путем деления произведения всех элементов на тот, который мы хотим исключить. Это самое простое решение задачи. И можно было бы тут заканчивать, однако в условиях есть требование, которое запрещает использовать операцию деления. Придется найти другое решение за линейное время.

Давайте посмотри на задачу под другим углом. Если визуализировать массив, то можно заметить, что каждый элемент (белый) разбивает массив на две части:

левая (желтая);
правая (голубая).

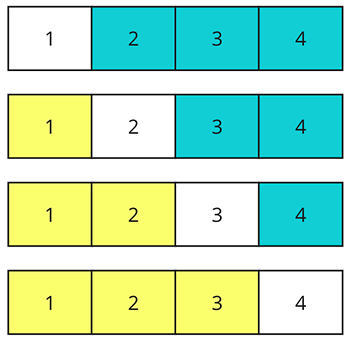
Левые и правые подмассивы

Исходя из этого, мы можем найти искомый результат следующим образом:

найти произведение всех элементов в левом подмассиве;
найти произведение всех элементов в правом подмассиве;
перемножить два полученных результата.

Алгоритм #

Инициализируем два пустых массива, left и right, где для каждого индекса left[i] будет содержать произведение всех чисел слева от i, а right[i] будет содержать произведение всех чисел справа от i.
Нам понадобятся два разных цикла для заполнения значений для двух массивов. Для массива left, первый элемент всегда будет равен 1, потому что слева от него нет других элементов. Для остальных элементов мы просто вычислим произведение следующим образом left[i] = left[i - 1] * nums[i - 1].
Для массива right мы делаем то же самое, но в обратном порядке. Последний элемент здесь также равен 1 так справа от него нет других элементов. Для остальных элементов мы просто вычислим произведение следующим образом right[i] = right[i + 1] * nums[i + 1].
И последним шагом нам осталось перемножить в цикле между собой каждый left[i] и right[i] элемент.

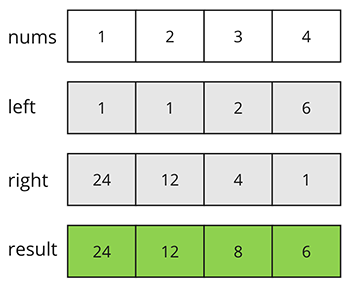
Для простоты восприятия визуализируем картинку.

Левые и правые подмассивы

Константная память #

Реализовать решение с константной памятью тоже не составит особых проблем, так как по условиям задачи создание массива с результатом не считается за выделение дополнительной памяти. В таком случае мы сначала в первом цикле создадим массив res и заполним его теми значениями, которые раньше были в left. И во втором цикле посчитаем правое произведение, которое раньше записывали в массив right. Однако в этот раз мы его запомним в отдельную переменную, а потом умножим на nums[i] (что по факту является left[i]) и сразу же перезапишем в nums[i].

Таким образом мы делаем всего два прохода по массиву и не выделяем дополнительную память, а все изменения производим in-place в результирующем массиве.

Реализация #

package main

func productExceptSelf(nums []int) []int {
	res := make([]int, len(nums))
	res[0] = 1

	for i := 1; i < len(nums); i++ {
		res[i] = res[i-1] * nums[i-1]
	}

	r := 1

	for i := len(nums) - 1; i >= 0; i-- {
		res[i] = r * res[i]
		r *= nums[i]
	}

	return res
}

// Хак, так как произведение отрицательного числа на 0 в JS дает -0
const multiply = (a: number, b: number): number => {
    const res = a * b
    return res === -0 ? 0 : res
}

export const productExceptSelf = (nums: number[]): number[] => {
    let res: number[] = []
    res[0] = 1

    for (let i = 1; i < nums.length; i++) {
        res[i] = multiply(res[i - 1], nums[i - 1])
    }

    let r = 1

    for (let i = nums.length - 1; i >= 0; i--) {
        res[i] = multiply(r, res[i])
        r *= nums[i]
    }

    return res
}

Оценка сложности #

По времени

n — количество элементов в массиве.

Сложность O(n) так как мы дважды перебираем n элементов массива, однако множитель 2 в оценке можно опустить.

По памяти

Сложность O(1), так как мы не выделяем дополнительную память.

Оригинал задачи на Leetcode

Algorithmics