Описание задачи #

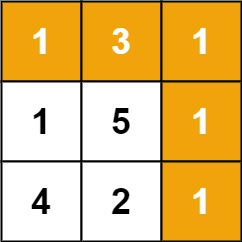
Напишите функцию, которая будет возвращать стоимость самого дешевого пути от левого верхнего элемента матрицы к нижнему правому. Значение ячейки матрицы — стоимость перехода в эту ячейку. Из каждой ячейки можно пойти либо вправо, либо вниз.

Входные данные: [][]int (матрица m на n в которой нужно искать путь)

Выходные данные: int (стоимость самого дешевого пути)

Ограничения #

• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

Примеры #

Брутфорс решение #

Это задача, тот случай, когда придумать реализацию брутфорс решение оказалось сложнее, чем оптимальное. Но, все же распишу, так как подобное решение может прийти в голову первым на собеседовании. Для брутфорс решения нам нужно сравнить все возможные пути между собой. Проще всего это сделать, превратив матрицу в граф. Введем вспомогательную структуру, чтобы превратить матрицу в граф.

type node struct {
	price    int
	children []*node
}

По условию задачи перейти в элемент графа (ячейку матрицы) можно либо из элемента слева от текущего, либо из верхнего элемента относительного текущего. Поэтому для правильного составления графа оставим вспомогательную матрицу (но, теперь, в качестве значений не int'ы, а ноды графа).

nodeGrid := make([][]node, 0, len(grid))

for i := 0; i < len(grid); i++ {
    nodeGrid = append(nodeGrid, make([]node, 0, len(grid[i])))
	
    for j := 0; j < len(grid[i]); j++ {
        nodeGrid[i] = append(nodeGrid[i], node{
            price:    grid[i][j],
            children: make([]*node, 0),
        })

        if i == 0 && j == 0 {
            continue
        }

        if i == 0 {
            nodeGrid[i][j-1].children = append(nodeGrid[i][j-1].children, &nodeGrid[i][j])
            continue
        }

        if j == 0 {
            nodeGrid[i-1][j].children = append(nodeGrid[i-1][j].children, &nodeGrid[i][j])
            continue
        }

        nodeGrid[i][j-1].children = append(nodeGrid[i][j-1].children, &nodeGrid[i][j])
        nodeGrid[i-1][j].children = append(nodeGrid[i-1][j].children, &nodeGrid[i][j])
    }
}

Теперь, имея граф с проставленными связями, мы можем с помощью обхода в глубину обойти все возможные пути от элемента nodeGrid[0][0] до элемента nodeGrid[m - 1][n - 1], сравнив стоимость путей.

func minPathSumTraverse(root node) int {
	if len(root.children) == 0 {
		return root.price
	}
	
	minPathPrice := math.MaxInt
	
	for _, child := range root.children {
		childPathPrice := minPathSumTraverse(*child)
		
		if childPathPrice < minPathPrice {
			minPathPrice = childPathPrice
		}
	}

	return root.price + minPathPrice
}

Оценка сложности #

По времени

Для того чтобы найти минимальный путь, нам нужно обойти все возможные пути в матрице. Каждый путь состоит из n+m-1 элементов. Длина каждого пути m+n-1, Не считая элементов первой/последней строки и первого/последнего столбца, из каждого элемента есть 2 пути. Суммарное количество возможных путей и сложность получившегося алгоритма можно оценить как O(2(n+m)).

По памяти

Мы ввели дополнительный граф размером m * n, поэтому дополнительную память мы можем оценить в O(m * n).

Оптимальное решение #

Оптимальное решение может получиться с использованием методов динамического программирования: мы разобьем задачу на более маленькие подзадачи.

Давайте предположим, что мы знаем самые дешевые пути от элемента матрицы grid[0][0] до элементов grid[n - 2][m - 1] (соседнего слева от правого нижнего элемента) и grid[n - 1][m - 2] (соседнего сверху от правого нижнего элемента).

Так как мы можем перемещаться либо вправо, либо вниз. Самый дешевый путь до правого нижнего элемента:

$$ grid[n-1][m-1] = min(grid[n-2][m-1], grid[n-1][m-2]) + grid[n-1][m-1] $$

Точно по такому же принципу мы можем вычислить самый короткий путь до элементов grid[n - 2][m - 1] и grid[n - 1][m - 2]. Таким образом, мы можем вычислить стоимость пути до каждого из элементов, зная стоимость пути до соседа слева и соседа сверху.

Давайте модифицируем исходную матрицу (так как нет требований к иммутабельности для экономии памяти будем менять значения в матрице in-place), преобразовав значение каждого из элементов в стоимости пути до этого элемента.

Для этого нам достаточно воспользоваться стандартным обходом матрицы в цикле по i и j. Первый элемент матрицы оставим без изменений, так как он является нашей отправной точкой.

Стоимость пути до любого элемента на первой строчке — стоимость пути до предыдущего элемента и значение текущего (так как к любому элементу на первой строке можно прийти только из элемента слева).

if i == 0 {
    grid[i][j] = grid[i][j-1] + grid[i][j]

    continue
}

Аналогичная проверка нужна для элементов первого столбца (можем прийти только с верхнего элемента).

if j == 0 {
    grid[i][j] = grid[i-1][j] + grid[i][j]

    continue
}

Для всех остальных элементов мы высчитываем стоимость, выбирая меньший из путей (либо сверху, либо слева).

minPrices := grid[i][j-1]
if grid[i-1][j] < minPrices {
    minPrices = grid[i-1][j]
}

grid[i][j] = minPrices + grid[i][j]

Таким образом, когда мы пройдемся по всей матрице в правом нижнем элементе будет вычислена стоимость самого дешевого пути до этого элемента. Итоговая реализация.

Оценка сложности #

По времени

Для того чтобы высчитать самый дешевый путь, нам достаточно один раз пройтись по всей матрице. То есть итоговая сложность — O(m * n).

По памяти

O(1) — дополнительная память константна.