Сколько нужно стрел, чтобы лопнуть все воздушные шары

Средняя

medium , string , backtracking

16 May 2024

Описание задачи #

К плоской стене, представляющей плоскость XY, приклеено несколько сферических воздушных шаров. Шары представлены в виде двумерного целочисленного массива points, где points[i] = [x_start, x_end] обозначает шар, горизонтальный диаметр которой простирается между x_start и x_end. Вы не знаете точных координат Y воздушных шаров.

Вы можете выстрелить стрелой прямо вертикально (в положительном направлении Y) из разных точек вдоль оси X. Воздушный шар с x_start, x_end разрывается стрелой, выпущенной в x, если x_start <= x <= x_end. Нет ограничений на количество выпущенных стрел.

Выпущенная стрела продолжает двигаться вверх бесконечно, разрывая все воздушные шары на своем пути. Найдите минимальное количество стрел, которое необходимо выпустить, чтобы лопнуть все воздушные шары.

Ограничения #

В массиве points может быть от 1 до 105 элементов
2³¹ <= x_start < x_end <= 2³¹ - 1

Примеры #

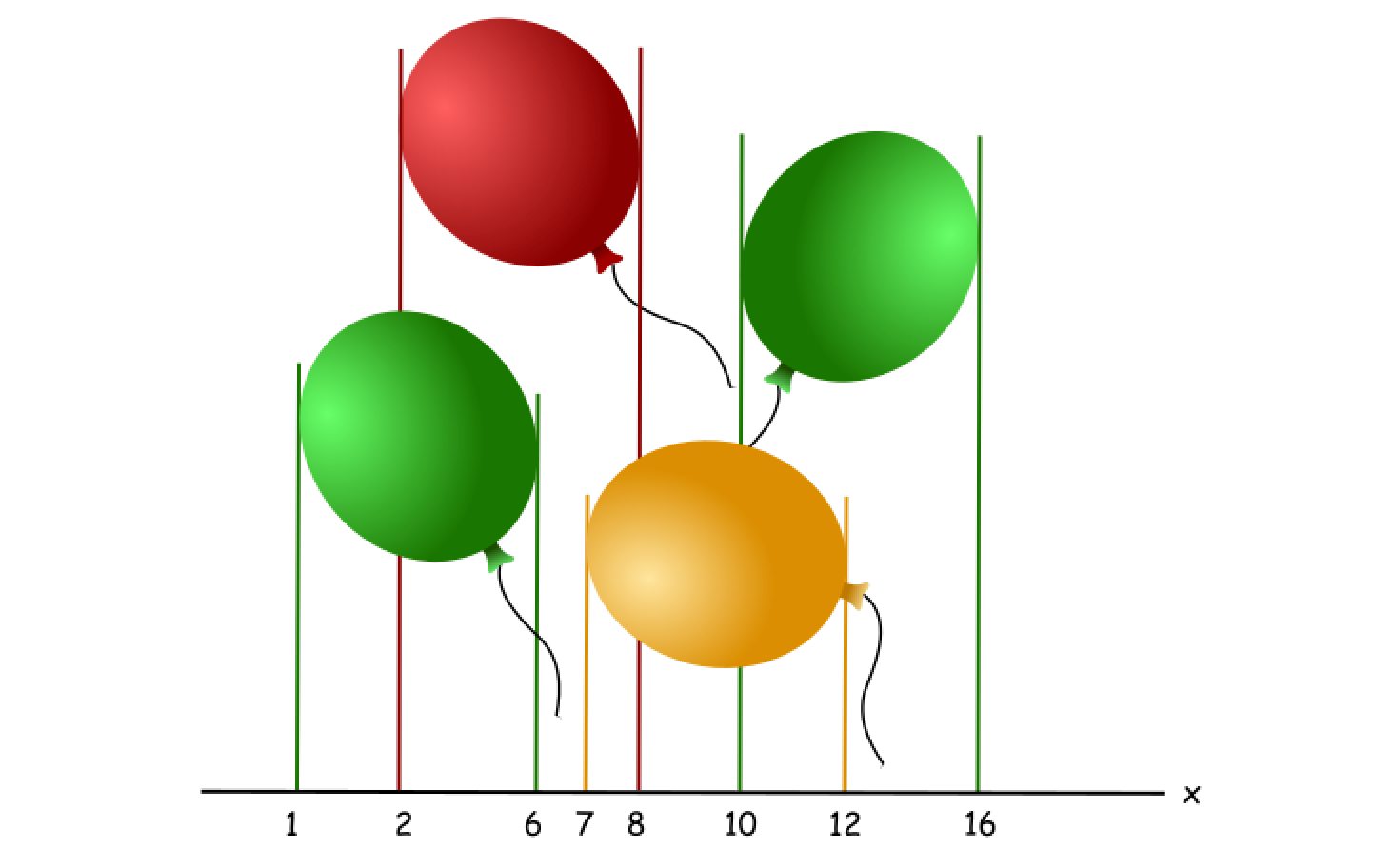
Входные данные: points = [[10,16],[2,8],[1,6],[7,12]]

Ответ: 2

Пояснение: Воздушные шары можно лопнуть двумя стрелами:
- Выстрелите стрелой в точку x = 6, лопнув шарики [2, 8] и [1, 6].
- Выстрелите стрелой в точку x = 11, лопнув шарики [10, 16] и [7, 12].
Входные данные: points = [[1,2],[3,4],[5,6],[7,8]]

Ответ: 4

Пояснение: Для каждого воздушного шара нужно выпустить одну стрелу, всего получится 4 стрелы.
Входные данные: points = [[1,2],[2,3],[3,4],[4,5]]

Ответ: 2

Пояснение: Воздушные шары можно лопнуть двумя стрелами:
- Выстрелите стрелой в точку x = 2, лопнув шарики [1, 2] и [2, 3].
- Выстрелите стрелой в точку x = 4, лопнув шарики [3, 4] и [4, 5].

Решение #

Шары

Для решения этой задачи первым делом надо отсортировать массив points по правой границе шаров. Такая сортировка поможет нам с легкостью определить, сколько стрел нужно выпустить, чтобы лопнуть все шары.

Если шары отсортированы по конечной координате, то мы знаем, что у следующего шара есть всего два варианта положения.

Его начальная координата больше конечной координаты текущего шара. В таком случае эти шары не пересекаются и их нельзя сбить одной стрелой.
Его начальная координата меньше или равна конечной координате текущего шара. В таком случае эти шары пересекаются и их можно сбить одной стрелой, если выстрелить в конечную координату текущего шара.

Исходя из этого мы можем сформировать крайне простой алгоритм:

Итерируемся по всем шарам в отсортированном массиве.
Запоминаем координату последнего выстрела, которую по умолчанию выставляем в минимально возможное значение.
Если начальная координата текущего шара больше координаты последнего выстрела, то это означает, что нам нужен сделать выстрел по правой границе шара и увеличить счетчик выпущенных стрел на 1.
Если начальная координата текущего шара меньше или равна координате последнего выстрела, то это означает, что шар пересекается с предыдущим и нам не нужно делать новый выстрел, потому что он уже был сбит предыдущей стрелой.

Реализация #

package minimum_number_of_arrows_to_burst_balloons

import (
	"math"
	"sort"
)

func findMinArrowShots(points [][]int) int {
	// Сортировка точек по второй координате каждой пары
	sort.Slice(points, func(i int, j int) bool {
		return points[i][1] < points[j][1]
	})

	count := 0
	lastShot := math.MinInt

	for _, cords := range points {
		if cords[0] > lastShot {
			count++
			lastShot = cords[1]
		}
	}

	return count
}

export const findMinArrowShots = (points: number[][]): number => {
    // Сортировка точек по второй координате каждой пары
    points.sort((a, b) => a[1] - b[1]);

    let count = 0;
    let lastShot = -Infinity;

    for (let cords of points) {
        if (cords[0] > lastShot) {
            count++;
            lastShot = cords[1];
        }
    }

    return count;
}

Оценка сложности #

По времени

O(n logn) — из-за сортировки массива points.

По памяти

Варьируется от O(n) до O(logn) в зависимости от реализации алгоритма сортировки. В остальном — потребление памяти константно.

Оригинал задачи на Leetcode

Algorithmics