Минимальное количество переворотов, чтобы сделать A | B == C

Средняя

medium , bit manipulation

07 June 2024

Описание задачи #

Даны три целых положительных числа a, b и c.

Необходимо найти минимальное количество переворотов битов в a и b, чтобы результат операции a OR b (побитовая операция ИЛИ) был равен c. Операция переворота состоит из изменения любого отдельного бита с 1 на 0 или c 0 на 1 в его двоичном представлении.

Ограничения #

Значение каждого аргумента находится в диапазоне от 1 до 10⁹

Примеры #

Входные данные: a = 2, b = 6, c = 5

Ответ: 3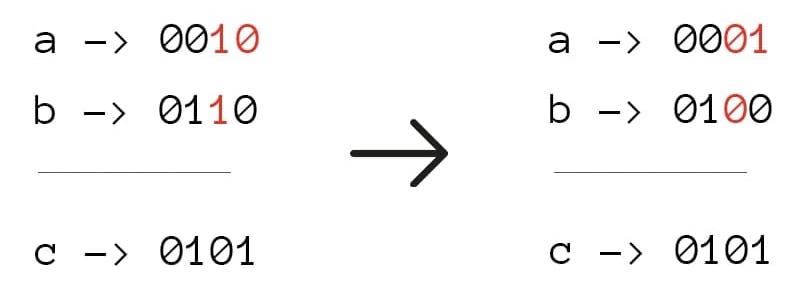

В исходных числах нужно поменять три бита, подсвеченных красным.
Входные данные: a = 4, b = 2, c = 7

Ответ: 1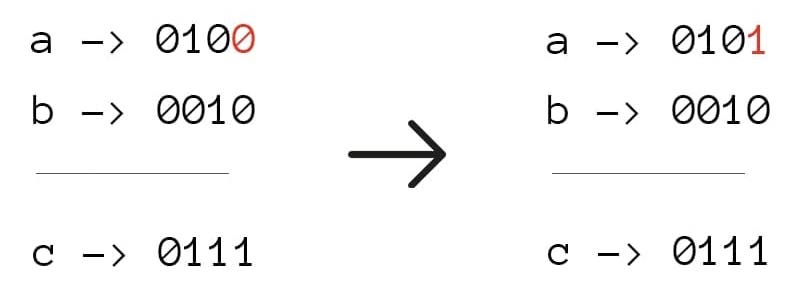

В исходных числах нужно поменять один бит, подсвеченный красным.
Входные данные: a = 1, b = 2, c = 3

Ответ: 0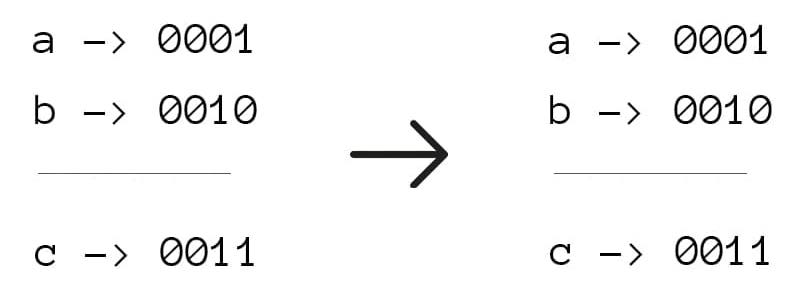

В исходных числах ничего не нужно менять, так как условие уже выполняется.

Решение #

Чтобы решить задачу, нам необходимо представить числа a, b и c в двоичном виде и произвести их сравнение побитно. Недостающие биты в числах мы заполняем ведущими нулями.

Если бит числа c равен 1, это означает, что в a и b как минимум один бит на этой же позиции должен быть равен 1, чтобы условие a | b == c было истинным. Если же оба бита в a и b равны 0, то нам необходимо изменить любой из битов на единицу. Не важно какой именно бит, потому что это не меняет результат.

Если бит числа c равен 0, это означает, что биты и в числе a, и в числе b должны быть равны нулю, чтобы условие a | b == c было истинным. В этом случае нам нужно изменять биты в a и b только в том случае, если они равны 1.

Как получить двоичное представление числа?

На самом деле число не нужно переводить в двоичную систему счисления. Достаточно воспользоваться небольшим математическим хаком.

Чтобы получить младший бит числа в двоичном представлении (крайний справа) необходимо взять остаток от деления числа на 2. Это работает потому что у четных чисел младший бит всегда равен 0, а у нечетных — 1.
Чтобы откинуть младший бит у числа достаточно разделить его на 2 без остатка. В таком случае мы получим новое число, которое в двоичном представлении равно предыдущему числу без младшего бита.

В итоге, нам необходимо иметь цикл, который проверяет младшие биты всех чисел на каждой итерации и увеличивает счетчик, а по завершению итерации модифицирует исходные числа. Этот цикл работает до тех пор, пока все числа не станут равны 0.

Реализация #

package main

func minFlips(a int, b int, c int) int {
	res := 0

	for a > 0 || b > 0 || c > 0 {
		bitA := a % 2
		bitB := b % 2
		bitC := c % 2

		a = a / 2
		b = b / 2
		c = c / 2

		if bitA|bitB == bitC {
			// Условие задачи выполняется, значит биты на этой позиции менять не нужно
			continue
		}

		if bitC == 0 {
			res += bitA + bitB
		} else {
			res += 1
		}
	}

	return res
}

export const minFlips = (a: number, b: number, c: number): number => {
    let res = 0;

    while (a > 0 || b > 0 || c > 0) {
        let bitA = a % 2;
        let bitB = b % 2;
        let bitC = c % 2;

        a = Math.floor(a / 2);
        b = Math.floor(b / 2);
        c = Math.floor(c / 2);

        if ((bitA | bitB) == bitC) {
            // Условие задачи выполняется, значит биты на этой позиции менять не нужно
            continue;
        }

        if (bitC == 0) {
            res += bitA + bitB;
        } else {
            res += 1;
        }
    }


    return res;
};

Оценка сложности #

n - количество элементов в строке.

По времени

Сложность по времени O(n), так как мы гарантированно найдем ответ, перебрав полностью всю строку один раз.

По памяти

Сложность по памяти O(1).

Оригинал задачи на Leetcode

Algorithmics