Максимальная глубина бинарного дерева

Легкая

20 June 2024

Описание задачи #

Найдите максимальную глубину бинарного дерева.

Максимальная глубина бинарного дерева — это количество узлов на самом длинном пути от корневого узла до самого дальнего листового узла.

Ограничения #

Количество узлов в дереве может быть от 0 до 10000
Значение каждого узла находится в диапазоне от -100 до 100

Примеры #

Входные данные:

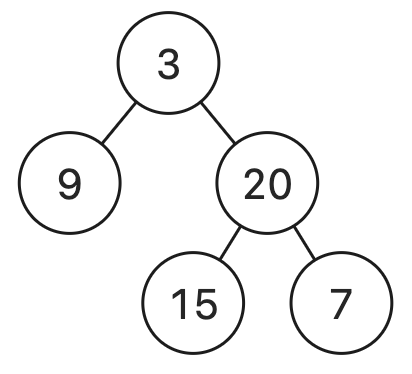
Ответ: 3
Входные данные:

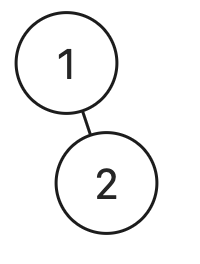
Ответ: 2

Решение #

Для решения задачи нам достаточно реализовать простой поиск в глубину DFS (Depth First Search).

Реализуем дополнительную рекурсивную функцию dfs, которая принимает на вход два аргумента:

текущий узел дерева node
текущую глубину погружения level

В качестве ответа функция будет возвращать максимальную глубину ветки дерева.

Если в функции dfs на вход пришла пустая нода, то это означает, что мы опустились ниже последнего листового узла в этой ветке, т. е. мы спустились до ее конца. В этом случае мы возвращаем из функции level в качестве ответа, так как он обозначает текущую глубину ветки.

Если же нода присутствует, то нам нужно найти в какой из ее дочерних веток максимальная глубина. Для этого мы запускаем рекурсивный поиск по левой и правой дочерней ветке и передаем в функцию увеличенный на 1 уровень глубины. Получив два числа для левой и правой ветки, нам нужно выбрать максимальное и вернуть его в качестве ответа.

В самом конце нам остается вызвать из основной функции maxDepth наш dfs поиск, определив начальную глубину равную 0.

Реализация #

package maximum_depth_of_binary_tree

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func maxDepth(root *TreeNode) int {
	return dfs(root, 0)
}

func dfs(root *TreeNode, level int) int {
	if root == nil {
		return level
	}

	leftDepth := dfs(root.Left, level+1)
	rightDepth := dfs(root.Right, level+1)

	if leftDepth > rightDepth {
		return leftDepth
	}

	return rightDepth
}

export type TreeNode = {
    val: number
    left: TreeNode | null
    right: TreeNode | null
}

export function maxDepth(root: TreeNode | null): number {
    return dfs(root, 0)
}

function dfs(node: TreeNode | null, level: number): number {
    if (!node) {
        return level
    }

    const leftDepth = dfs(node.left, level + 1)
    const rightDepth = dfs(node.right, level + 1)

    return Math.max(leftDepth, rightDepth)
}

Оценка сложности #

По времени

O(n), так как нам нужно перебрать все элементы в дереве.

По памяти

Хоть мы и не выделяем напрямую дополнительную память, которая напрямую зависит от размера входящих данных, однако задача решается через рекурсию. Это означает, что результат самого первого вызова не будет получен, до тех пор, пока не будут получены результаты всех вложенных рекурсивных вызовов. То есть мы будем хранить в памяти n вызовов кол стека. Поэтому сложность по памяти равна O(n).

Оригинал задачи на Leetcode

Algorithmics