Максимальный зигзагообразный путь в бинарном дереве

Средняя

01 March 2024

Описание задачи #

Напишите функцию, которая будет вычислять длину самого длинного зигзагообра́зного пути в бинарном дереве. Путь может начинаться НЕ с корневого элемента дерева.

Входные данные

Ссылка на корневой элемент бинарного дерева.

Выходные данные

Длина максимального участка зигзагообра́зного пути.

Ограничения #

Количество элементов в дереве от 1 до 50000

Пример #

Входные данные:

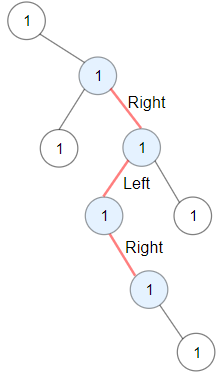
Ответ: 3
Входные данные:

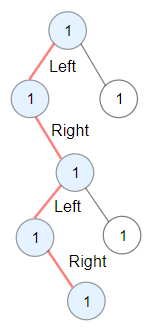
Ответ: 4

Решение #

Для решения данной задачи нам придется вспомнить как работает алгоритм DFS в деревьях и немного модифицировать его.

Нам нужно, чтобы поиск в глубину возвращал длину зигзага, который начинается слева от текущего элемента и справа. Тогда, поднимаясь по дереву, мы легко сможем посчитать длину пути (необходимо помнить, что если мы идем от текущего элемента вправо, то от дочернего должны обязательно пойти влево и наоборот):

Для каждого элемента дерева длина зигзага начинающегося с этого элемента налево равна длине зигзага дочернего элемента справа + 1
Для каждого элемента дерева длина зигзага начинающегося с этого элемента направо равна длине зигзага дочернего элемента слева + 1

Если бы условия позволяли начинать путь только от корневого элемента, то нам бы хватило этих двух величин и на выходе нам нужно было только сравнить их между собой и вернуть максимум. Но в данной задаче нам придется оперировать третьим параметром, чтобы не потерять дочерние пути (для простоты назовем его maxLength).

В этот параметр для каждого элемента мы будем складывать максимум из четырех значений:

Длину зигзага, начинающегося от текущего элемента направо.
Длину зигзага, начинающегося от текущего элемента налево.
maxLength дочернего элемента слева
maxLength дочернего элемента справа

Таким образом этот параметр позволит «всплывать» длинным путям дочерних элементов, чей зиг заг был «оборван» при подъеме по дереву во время поиска в глубину.

Реализация #

package main

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func longestZigZag(root *TreeNode) int {
	_, _, m := dfs(root)

	return m
}

func dfs(root *TreeNode) (int, int, int) {
	var leftPathLength, rightPathLength, leftMaxLength, rightMaxLength int
	if root == nil {
		return leftPathLength, rightPathLength, 0
	}

	if root.Left != nil {
		var childRightZigZag int
		_, childRightZigZag, leftMaxLength = dfs(root.Left)
		leftPathLength = childRightZigZag + 1
	}

	if root.Right != nil {
		var childLeftZigZag int
		childLeftZigZag, _, rightMaxLength = dfs(root.Right)

		rightPathLength = childLeftZigZag + 1
	}

	maxLength := max(max(leftMaxLength, rightMaxLength), max(leftPathLength, rightPathLength))
	return leftPathLength, rightPathLength, maxLength
}

export type TreeNode = {
    val: number
    left?: TreeNode
    right?: TreeNode
}

type DFSResult = {
    leftPathLength: number
    rightPathLength: number
    maxLength: number
}

const dfs = (root?: TreeNode): DFSResult => {
    if (!root) {
        return {
            leftPathLength: 0,
            rightPathLength: 0,
            maxLength: 0,
        }
    }

    let leftPathLength = 0
    let rightPathLength = 0
    let leftMaxLength = 0
    let rightMaxLength = 0

    if (root.left) {
        const leftDFSRes = dfs(root.left)
        leftPathLength = leftDFSRes.rightPathLength + 1
        leftMaxLength = leftDFSRes.maxLength
    }

    if (root.right) {
        const rightDFSRes = dfs(root.right)
        rightPathLength = rightDFSRes.leftPathLength + 1
        rightMaxLength = rightDFSRes.maxLength
    }

    const maxLength = Math.max(Math.max(leftMaxLength, rightMaxLength), Math.max(leftPathLength, rightPathLength))

    return {
        leftPathLength,
        rightPathLength,
        maxLength,
    }
}

export const longestZigZag = (root?: TreeNode): number => {
    const { maxLength} = dfs(root)
    return maxLength
}

Оценка сложности #

По времени

O(n) — так как нам нужно совершить поиск в глубину по бинарному дереву, перебрав все n его элементов.

По памяти

O(n) — так как мы используем рекурсивный подход.

Это означает, что мы будем хранить в памяти n переменных во время вычисления стека рекурсии.

Оригинал задачи на Leetcode

Algorithmics