Листоподобные деревья

Легкая

25 June 2024

Описание задачи #

Дано два бинарных дерева.

Все листовые узлы дерева образуют последовательность значений.

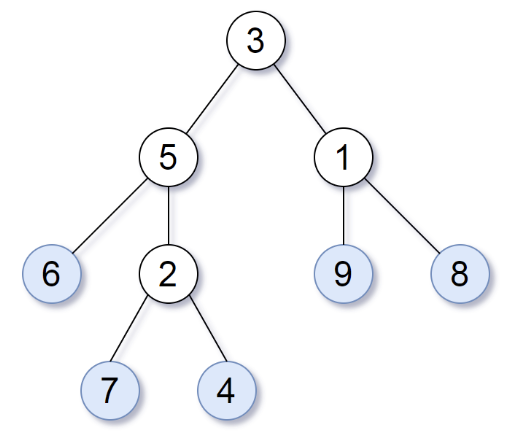
Последовательность значений листьев

Например, для дерева выше последовательность значений будет равна (6, 7, 4, 9, 8).

Два бинарных дерева считаются листоподобными, если последовательность значений их листьев одинакова.

Напишите функцию, которая возвращает true тогда и только тогда, когда два заданных дерева являются листоподобными.

Ограничения #

Количество узлов в каждом дереве находится в диапазоне [1, 200]
Узлы обоих деревьев имеют значения в диапазоне [0, 200]

Примеры #

Входные данные:

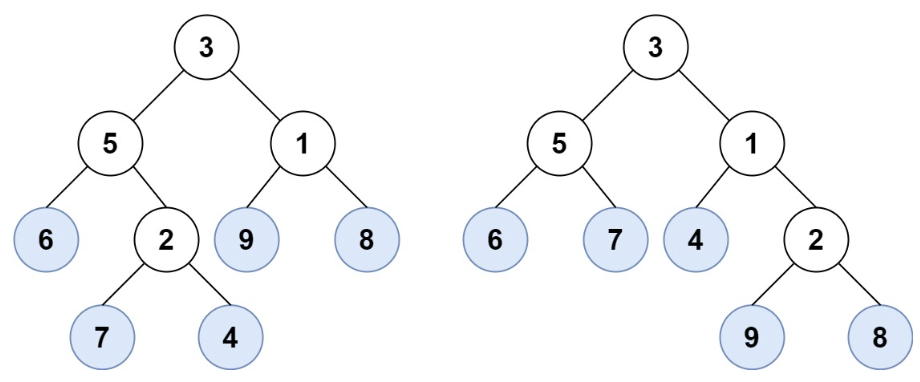
Ответ: true
Входные данные:

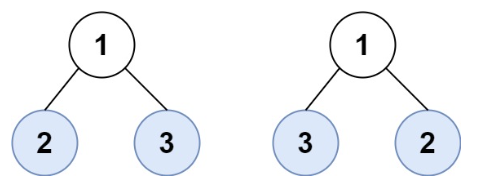
Ответ: false

Решение #

Для решения задачи нам необходимо собрать последовательность всех листовых узлов в обоих деревьях и сравнить их.

Для этого мы реализуем отдельную функцию getSequence, которая будет формировать последовательность значений листовых узлов для переданного дерева.

Функция осуществляет классический обход дерева в глубину DFS (Depth First Search) и когда встречает листовой узел (узел, у которого нет потомков), то добавляет его значение в строку sequence, разделяя значения точкой с запятой. Предварительно мы определяем переменную sequence, равную пустой строке, и управляем ее значением через замыкание.

Вместо строки можно было бы использовать массивы, но после вычисления массивом их пришлось бы сравнивать итерируясь по всем элементам, что дало бы дополнительных k операций. Строки же можно просто сравнить между самой через ==.

Реализация #

package leaf_similar_trees

import (
	"fmt"
	"strconv"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func leafSimilar(root1 *TreeNode, root2 *TreeNode) bool {
	first := getSequence(root1)
	second := getSequence(root2)

	return first == second
}

func getSequence(root *TreeNode) string {
	var dfs func(node *TreeNode)

	sequence := ""

	dfs = func(node *TreeNode) {
		if node.Left == nil && node.Right == nil {
			fmt.Println(node.Val)
			sequence += strconv.Itoa(node.Val) + ";"
		}

		if node.Left != nil {
			dfs(node.Left)
		}

		if node.Right != nil {
			dfs(node.Right)
		}
	}

	dfs(root)

	return sequence
}

export type TreeNode = {
    val: number
    left: TreeNode | null
    right: TreeNode | null
}

export function leafSimilar(root1: TreeNode | null, root2: TreeNode | null): boolean {
    if (!root1 || !root2) {
        return false
    }

    const first = getSequence(root1)
    const second = getSequence(root2)

    return first === second
}

function getSequence(root: TreeNode): string {
    let sequence = ""

    const dfs = (node: TreeNode): void => {
        if (!node.left && !node.right) {
            sequence = `${sequence}${node.val};`
        }

        if (node.left) {
            dfs(node.left)
        }

        if (node.right) {
            dfs(node.right)
        }
    }

    dfs(root)

    return sequence
}

Оценка сложности #

n1 — количество узлов в первом дереве
n2 — количество узлов во втором дереве
h1 — высота первого дерева
h2 — высота второго дерева

По времени

O(n1 + n2), так как нам нужно перебрать все элементы в дереве.

По памяти

Так как мы храним последовательности листовых узлов в виде строки, то выделяемую память мы считаем константной. Однако, это рекурсивный алгоритм поэтому нужно учесть память используемую стеком вызовов.

Таким образом сложность по памяти равна O(h1 + h2).

Оригинал задачи на Leetcode

Algorithmics