Игра в жизнь

Средняя

medium , matrix , simulation

10 October 2023

Описание задачи #

Механика игры подробно описана в статье на википедии.

Доска состоит из сетки ячеек размером m x n, где каждая ячейка имеет начальное состояние:

живое — обозначается цифрой 1
мертвое — обозначается цифрой 0.

Каждая ячейка взаимодействует со своими восемью соседями (горизонтальными, вертикальными, диагональными), используя следующие четыре правила.

Любая живая клетка, имеющая менее двух живых соседей, умирает, как из-за недостаточной численности населения.
Любая живая клетка с двумя или тремя живыми соседями доживает до следующего поколения.
Любая живая клетка, имеющая более трех живых соседей, погибает от перенаселения.
Любая мертвая клетка, имеющая ровно три живых соседа, становится живой клеткой путем размножения.

Следующее состояние доски создается путем одновременного применения вышеуказанных правил к каждой ячейке в текущем состоянии, где рождение и смерть происходят одновременно.

Напишите функцию, которая принимает на вход матрицу состояния и изменяет ее до следующего состояния.

Ограничения #

m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] == 0 || board[i][j] == 1

Примеры #

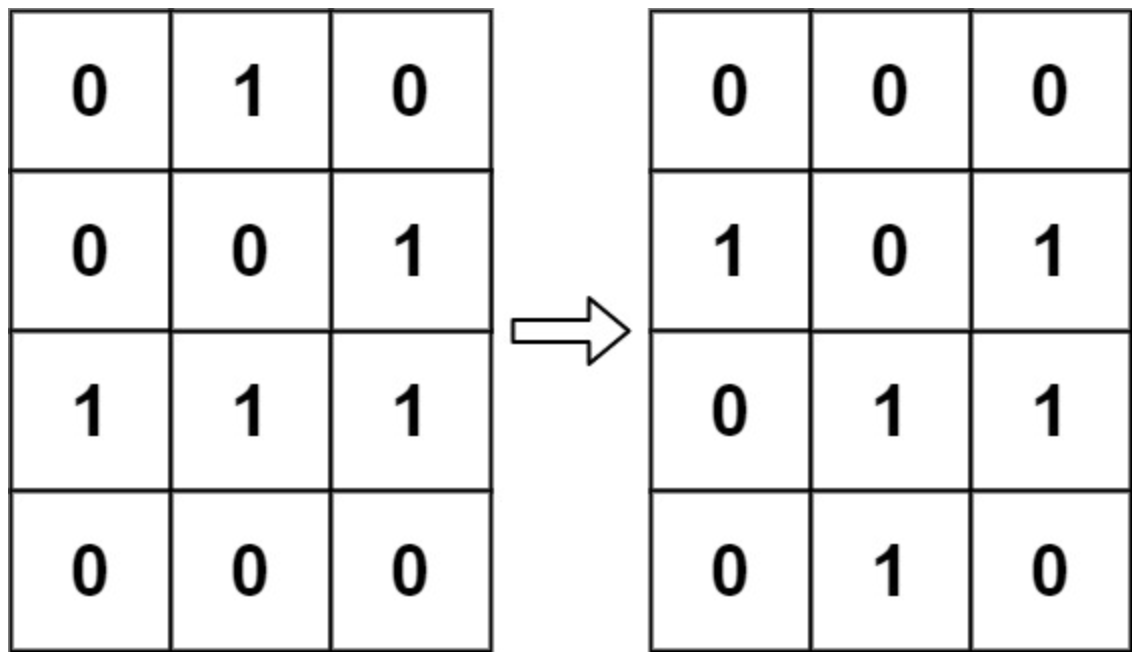
Пример 1

Входные данные

[
    [0, 1, 0],
    [0, 0, 1],
    [1, 1, 1],
    [0, 0, 0],
]

Ответ

[
    [0, 0, 0],
    [1, 0, 1],
    [0, 1, 1],
    [0, 1, 0],
]

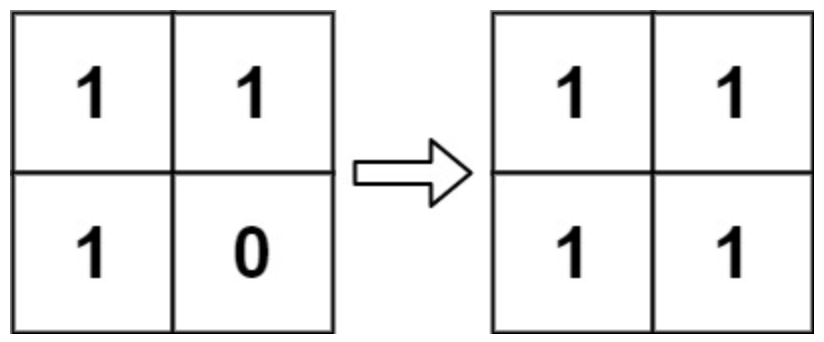
Пример 1

Входные данные

[
    [1, 1],
    [1, 0],
]

Ответ

[
    [1, 1],
    [1, 1],
]

Решение #

Эту задачу очень просто решить, если реализовать изменение матрицы в ее копии. Это делает алгоритм очень простым, но требует выделения дополнительной памяти, что может стать проблемой при большом количестве данных.

Чтобы иметь оптимальное потребление памяти, нужно производить все изменения in-place. Если мы будем просто менять состояние в исходной матрице при проверке каждого элемента, то мы потеряем исходное состояние и не сможем корректно проверять необходимость мутации.

Для того чтобы это обойти введем два новых значения для матрицы.

2 обозначает переход нуля в единицу. Мы будем использовать двойку в качестве значения, чтобы пометить неживые клетки, которые должны стать живыми по итогам наших расчетов.
3 обозначает переход единицы в ноль. Мы будем использовать тройку в качестве значения, чтобы пометить живые клетки, которые должны стать неживыми по итогам наших расчетов.

При вычислении состояния для каждой клетки нужно учитывать эти нововведения. В конце после того, как мы поменяем состояния для всех элементов матрицы нужно еще раз обновить ее и заменить все 2 на 0, а 3 на 1.

package main

func gameOfLife(board [][]int) {
	for i := 0; i < len(board); i++ {
		for j := 0; j < len(board[i]); j++ {
			count := liveCount(board, i, j)

			if board[i][j] == 0 {
				if count == 3 {
					board[i][j] = 2
				}

				continue
			}

			if count < 2 || count > 3 {
				board[i][j] = 3
				continue
			}

			board[i][j] = 1
		}
	}

	for i := 0; i < len(board); i++ {
		for j := 0; j < len(board[i]); j++ {
			if board[i][j] == 3 {
				board[i][j] = 0
			}

			if board[i][j] == 2 {
				board[i][j] = 1
			}
		}
	}
}

func liveCount(board [][]int, i, j int) int {
	up, down, in := 0, 0, 0

	if i > 0 {
		up = getValue(board[i-1][j])

		if j > 0 {
			up += getValue(board[i-1][j-1])
		}

		if j < len(board[i])-1 {
			up += getValue(board[i-1][j+1])
		}
	}

	if i < len(board)-1 {
		down = getValue(board[i+1][j])

		if j > 0 {
			up += getValue(board[i+1][j-1])
		}

		if j < len(board[i])-1 {
			up += getValue(board[i+1][j+1])
		}
	}

	if j > 0 {
		in += getValue(board[i][j-1])
	}

	if j < len(board[i])-1 {
		in += getValue(board[i][j+1])
	}

	return up + down + in
}

func getValue(val int) int {
	if val == 2 {
		return 0
	}

	if val == 3 {
		return 1
	}

	return val
}

export const gameOfLife = (board: number[][]): void => {
    for (let i = 0; i < board.length; i++) {
        for (let j = 0; j < board[i].length; j++) {
            const count = liveCount(board, i, j)

            if (board[i][j] == 0) {
                if (count == 3) {
                    board[i][j] = 2
                }

                continue
            }

            if (count < 2 || count > 3) {
                board[i][j] = 3
                continue
            }

            board[i][j] = 1
        }
    }

    for (let i = 0; i < board.length; i++) {
        for (let j = 0; j < board[i].length; j++) {
            if (board[i][j] == 3) {
                board[i][j] = 0
            }

            if (board[i][j] == 2) {
                board[i][j] = 1
            }
        }
    }
}

function liveCount(board: number[][], i: number, j: number): number {
    const m = board[i].length
    const n = board.length
    
    let up = 0;
    let down = 0;
    let sides = 0;

    if (i > 0) {
        up = getValue(board[i - 1][j])

        if (j > 0) {
            up += getValue(board[i - 1][j - 1])
        }

        if (j < m - 1) {
            up += getValue(board[i - 1][j + 1])
        }
    }

    if (i < n - 1) {
        down = getValue(board[i + 1][j])

        if (j > 0) {
            up += getValue(board[i + 1][j - 1])
        }

        if (j < m - 1) {
            up += getValue(board[i + 1][j + 1])
        }
    }

    if (j > 0) {
        sides += getValue(board[i][j - 1])
    }

    if (j < m - 1) {
        sides += getValue(board[i][j + 1])
    }

    return up + down + sides
}

function getValue(val: number): number {
    if (val == 2) {
        return 0
    }

    if (val == 3) {
        return 1
    }

    return val
}

Оценка сложности #

По времени

O(m * n) так как мы обходим всю матрицу поэлементно.

По памяти

O(1) так как мы не выделяем дополнительную память.

Оригинал задачи на Leetcode

Algorithmics