Disjoint Set

data_structure , graph , disjoint_set
03 February 2025

В этом посте мы с вами не будем решать конкретную задачу, а познакомимся с новой структурой данных.

Представим, что перед нами есть карта, на которой схематично обозначены 8 городов. При этом, города 0, 1, 2 и 3 соединены между собой дорогами. Города 4, 5 и 6 также соединены между собой, а город 7 обособлен и не имеет сообщения с другими.

Таким образом города являются вершинами графов, а дороги — их ребрами.

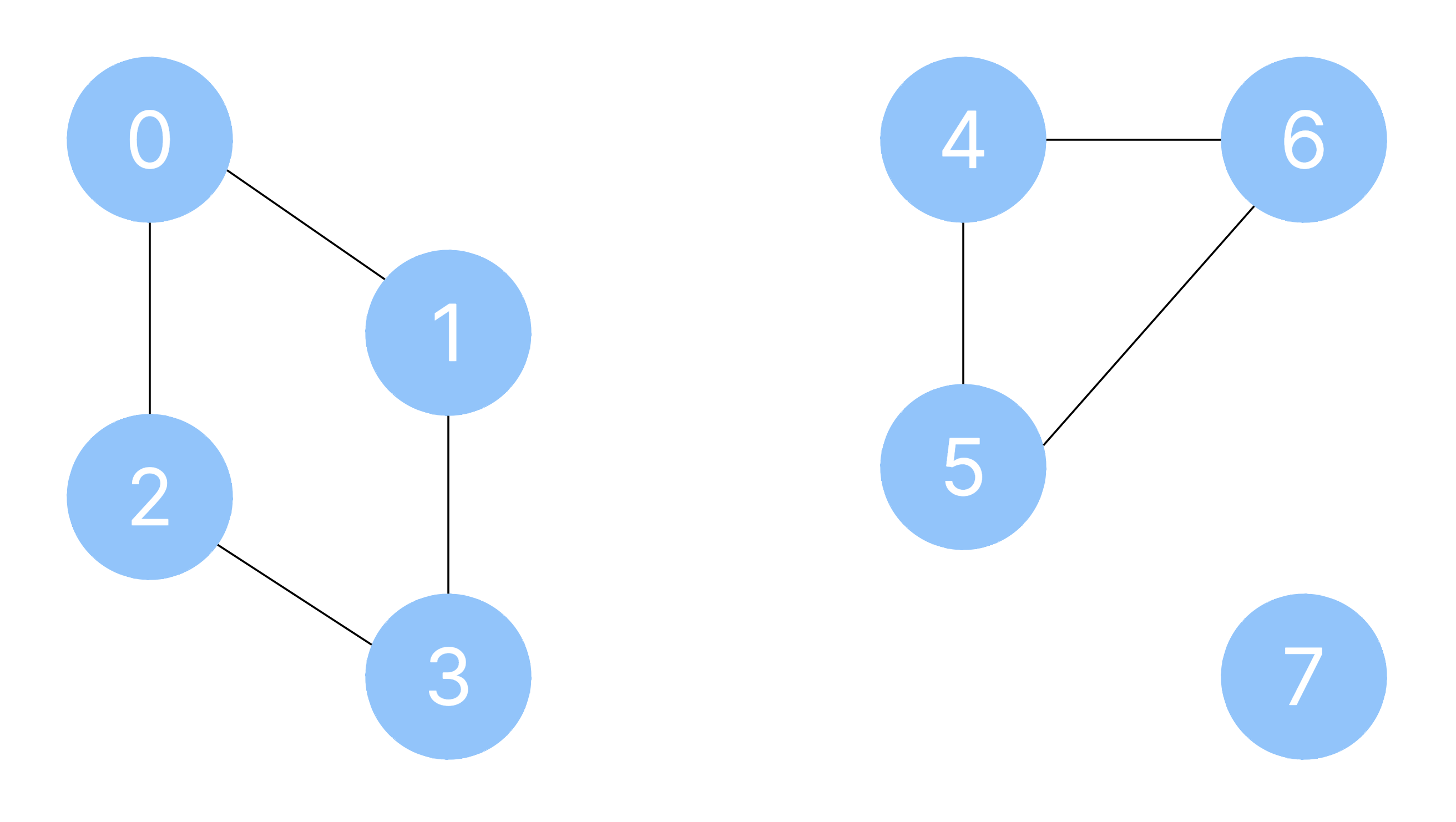
Схематичная карта городов

Города могут иметь прямое соединение, как например 4 и 6, или же транзитивное как в случае 0 и 3. В результате мы имеем три непересекающихся множества:

Теперь нам нужно построить эффективную структуру, которая позволит быстро понимать, соединены ли два города между собой, и даст возможность объединять два непересекающихся множества в одно.

Для подобных задач можно использовать структуру данных Disjoint Set, которую также иногда называют Union Find.

Базовая реализация #

Базово такая структура данных должна поддерживать три основных метода

Внутри структура будет хранить связи между вершинами графа в виде массива, где индекс массива обозначает номер города, а значение по индексу — индекс рутового узла в графе.

Таким образом для нашего случая массив должен иметь следующий вид.

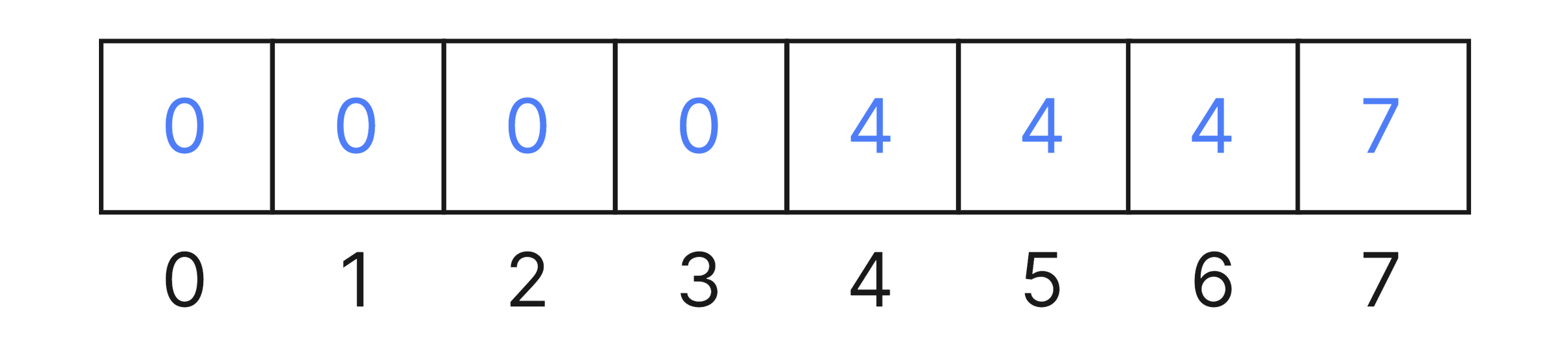
Схематичная карта городов

Поиск #

Теперь не сложно догадаться, что для реализации поиска достаточно получить индекс рутового узла для конкретного города по его индексу в массиве.

Проверка связности #

Проверка связности тоже реализуется крайне легко. Нужно получить рутовые элементы для города x и y при помощи метода find и сравнить их. Если два города имеют один и тот же рутовый город в графе, то они связаны либо напрямую, либо транзитивно.

Объединение множеств #

Теперь предположим, что нам нужно соединить города с номерами 3 и 4, тем самым объединив первое и второе множества.

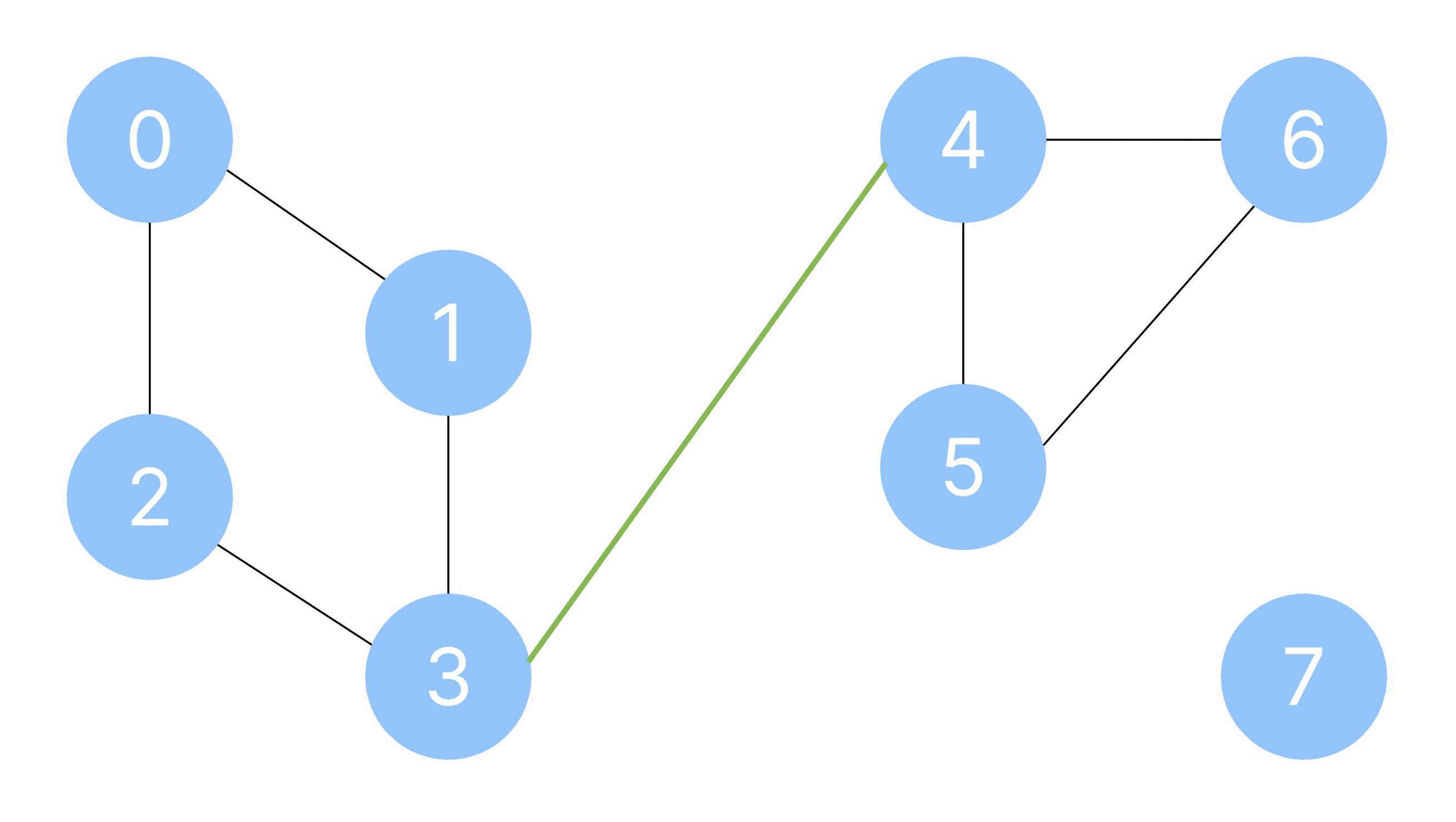
Схематичная карта городов

Мы решаем, что у объединенного множества родительский элемент остается равным 0. Это означает, что города с номерами 3, 4 и 5 должны получить связь с ним, то есть обновить значение своего рутового узла на 0.

Таким образом наш массив должен получить следующие значения.

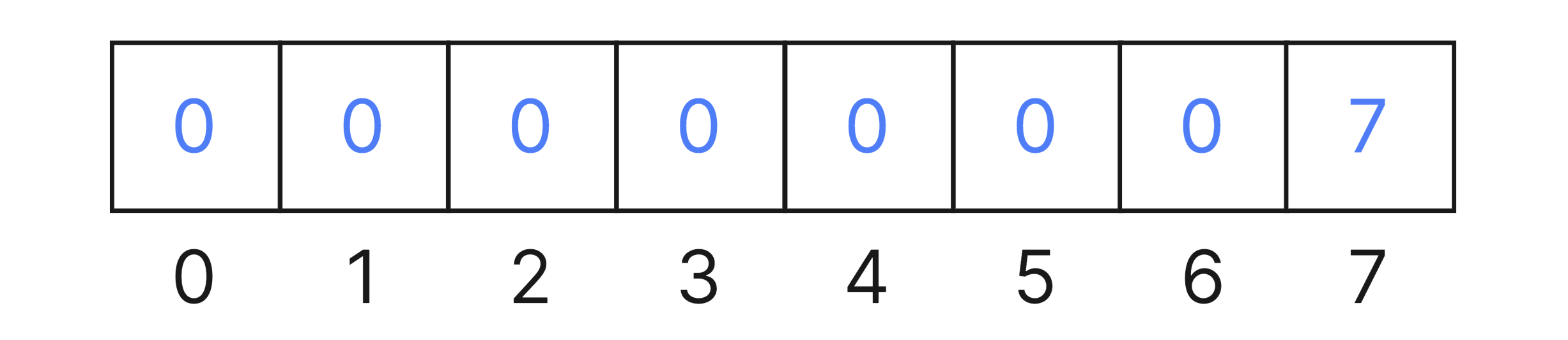
Схематичная карта городов

Реализация #

Теперь осталось имплементировать структуру данных по описанной логике.

  • package disjoint_set

type DisjointSet struct {
	// Представление графа в виде слайса
	nodes []int
}

func NewDisjointSet(n int) DisjointSet {
	// Создаем слайс заданного размера по количеству элементов
	nodes := make([]int, n)

	for i := 0; i < n; i++ {
		// При инициализации считаем что каждый элемент обособлен и не соединен с другими.
		// В таком случае каждый элемент является рутовым сам для себя
		nodes[i] = i
	}

	return DisjointSet{
		nodes: nodes,
	}
}

func (uf *DisjointSet) find(node int) int {
	return uf.nodes[node]
}

func (uf *DisjointSet) connected(x int, y int) bool {
	return uf.find(x) == uf.find(y)
}

func (uf *DisjointSet) union(x int, y int) {
	rootX := uf.find(x)
	rootY := uf.find(y)

	// Производим объединение только если два элемента находятся не в одном множестве и не имеют одинаковый рутовый узел.
	if rootY != rootX {
		for i := range uf.nodes {
			// Обновляем значение рутового элемента на новое у всех элементов второго множества
			if uf.nodes[i] == rootY {
				uf.nodes[i] = rootX
			}
		}
	}
}

  • export class DisjointSet {
    readonly nodes: number[];

    constructor(size: number) {
        // Создаем массив заданного размера по количеству элементов
        this.nodes = new Array(size);

        for (let i = 0; i < size; i++) {
            // При инициализации каждый элемент является рутовым сам для себя
            this.nodes[i] = i;
        }
    }

    find(node: number): number {
        return this.nodes[node];
    }

    connected(x: number, y: number): boolean {
        return this.find(x) === this.find(y);
    }

    union(x: number, y: number): void {
        const rootX = this.find(x);
        const rootY = this.find(y);

        // Объединяем множества, если они не совпадают
        if (rootX !== rootY) {
            for (let i = 0; i < this.nodes.length; i++) {
                if (this.nodes[i] === rootY) {
                    this.nodes[i] = rootX;
                }
            }
        }
    }
}

А в качестве проверки нашей реализации напишем несколько простых тестов.

  • func Test_DisjointSet(t *testing.T) {
	set := NewDisjointSet(8)

    // Наполняем структуру данными о связях между городами
    set.union(0, 2)
	set.union(0, 1)
	set.union(2, 3)
	set.union(1, 3)

	set.union(4, 5)
	set.union(4, 6)
	set.union(5, 6)

	t.Run("Create disjoint set", func(t *testing.T) {
		assert.Equal(t, []int{0, 0, 0, 0, 4, 4, 4, 7}, set.nodes)
		assert.Equal(t, 4, set.find(5))
	})

	t.Run("Check union", func(t *testing.T) {
		set.union(3, 4)
		assert.Equal(t, set.nodes, []int{0, 0, 0, 0, 0, 0, 0, 7})
		assert.Equal(t, set.connected(0, 6), true)
	})
}
  • describe('DisjointSet', () => {
    const set = new DisjointSet(8)
    
    // Наполняем структуру данными о связях между городами
    set.union(0, 2)
    set.union(0, 1)
    set.union(2, 3)
    set.union(1, 3)
    
    set.union(4, 5)
    set.union(4, 6)
    set.union(5, 6)

    test("Create disjoint set", () => {
        expect(set.nodes).toEqual([0, 0, 0, 0, 4, 4, 4, 7]);
        expect(set.find(5)).toEqual(4);
    })

    test("Check union", () => {
        set.union(3, 4)
        expect(set.nodes).toEqual([0, 0, 0, 0, 0, 0, 0, 7]);
        expect(set.connected(0, 6)).toEqual(true);
    })
})

Оценка сложности #

Теперь оценим сложность каждого метода созданной нами структуры данных.

По времени

По памяти

Сложность O(n) для всех методов, так как мы создаем массив nodes длинною n для хранения значений.

< Предыдущая задача
Следующая задача >