Описание задачи #

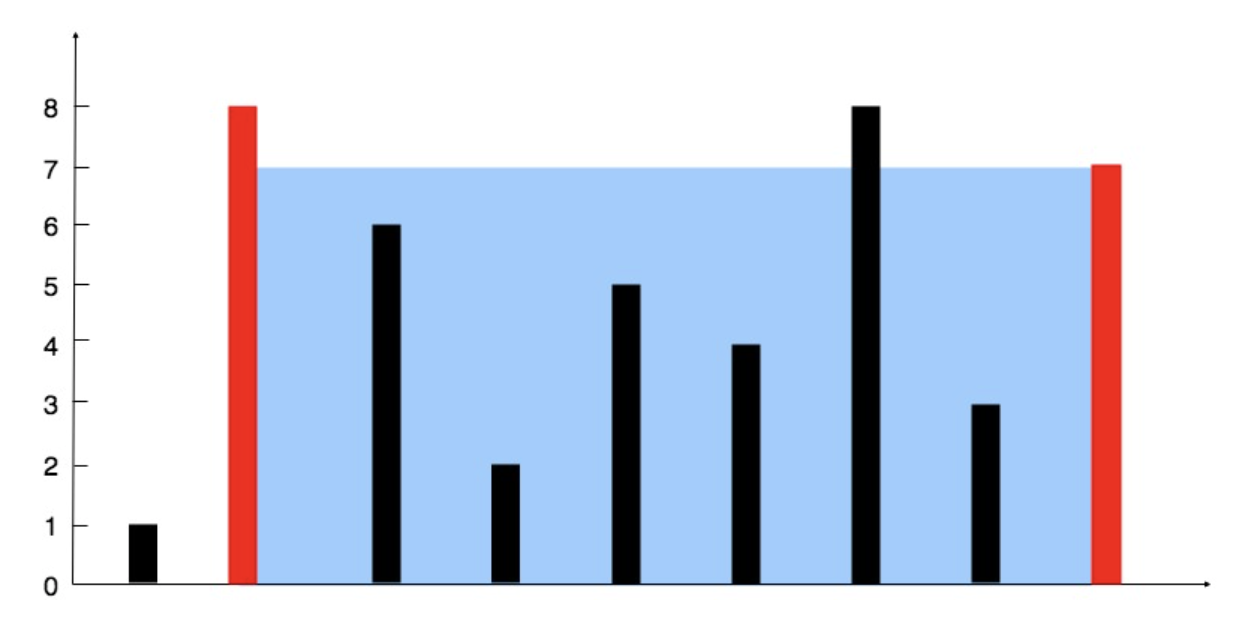
Вам дан целочисленный массив высот height длиною n.

Найдите две линии, которые вместе с осью X образуют контейнер, в котором содержится больше всего воды. Верните из функции максимальное количество воды, которое может хранить контейнер.

Задача сводится к поиску прямоугольника максимальной площади.

Ограничения #

• В массиве всегда есть минимум 2 элемента
• Значения элементов могут быть в диапазоне от 0 до 10⁴

Примеры #

Брутфорс решение #

Задачу можно разделить на 2 этапа:

• поиск всех возможных площадей всех возможных прямоугольников с сохранением результатов в промежуточный массив;
• поиск максимума в массиве.

Вычисление всех возможных площадей прямоугольников:

squares := make([]int, 0, len(height)*len(height))

for i := 0; i < len(height)-1; i++ {
    for j := i + 1; j < len(height); j++ {
        minHeight := height[i]
        if height[j] < minHeight {
            minHeight = height[j]
        }

        squares = append(squares, minHeight*(j-i))
    }
}

Поиск максимума:

res := 0
for _, square := range squares {
    if square > res {
        res = square
    }
}

Небольшие улучшения #

Можно заметить, что для вычисления максимумов нам нет нужды сохранять площади в промежуточный массив, мы можем проверять сравнивать и сохранять максимальную площадь в момент расчета:

func maxArea(height []int) int {
  res := 0
  for i := 0; i < len(height)-1; i++ {
      for j := i + 1; j < len(height); j++ {
          minHeight := height[i]
          if height[j] < minHeight {
              minHeight = height[j]
          }
          
          square := minHeight*(j-i)
          if square > res {
              res = square
          }
      }
  }

  return res
}

Таким образом мы избавляемся от необходимости хранить дополнительный массив squares размером n2 и отдельно вычислять максимумы в этом массиве и при этом уменьшаем сложность алгоритма по памяти с квадратичной до константной.

P.S. Несмотря на то, что мы избавились от дополнительного обхода массива squares, на итоговую сложность алгоритма по времени это не повлияло, так в оценке нам важен порядок роста, который остался прежним, так как мы все еще обходим входящий массив «циклом в цикле».

Улучшаем алгоритм дальше #

Можно попробовать еще немного улучшить алгоритм, отбросив заведомо лишние действия. Для этого вложенный цикл запустим не от следующего за i элемента, а от максимально далекого. Таким образом мы сперва проверяем прямоугольники с максимальной длиной. В этом случае мы сможем добавить условие выхода из внутреннего цикла (не уменьшать дальше длины прямоугольника, так как все прямоугольники с меньшей длинной при заданном i окажутся заведомо меньшей площади).

length := j - i

if length * height[i] < res {
    break
}

В итоге мы получим следующее решение.

Оценка сложности #

По времени

Для того чтобы вычислить все возможные площади, необходимо перебрать все возможные комбинации 2-х элементов в массиве. Это сводится к «циклу в цикле», что можно прировнять к сложности O(n2)

Для того чтобы найти максимум в массиве, нужно перебрать весь получившийся массив один раз. Так как массив squares имеет размер ~n², то сложность также сводится к O(n2).

То есть суммарная оценка O(n2) + O(n2) = O(2n2)

Так как при оценке алгоритма нам важен только порядок роста функции (т.е. приниматься будет только главный член формулы без учета константных множителей), итоговая оценка - O(n2)

По памяти

Сложность по памяти константная O(1).

Решение через скользящее окно #

Для решения подобных задач оптимальным подходом может оказаться «скользящее окно». Идея состоит в том, чтобы выбрать некое окно и в зависимости от условий сдвигать одну или обе границы окна в сторону.

В нашем случае в качестве первоначального «окна» мы можем взять весь массив. Так же как и в улучшенном брутфорсе начинаем с прямоугольника максимальной длины. Окно мы будем сужать, пока не дойдем до единичного отрезка в длину. Так как в качестве первоначального окна мы берем прямоугольник с максимальной длиной, то единственный способ получить прямоугольник большей площади при уменьшении длины — увеличение высоты.

Таким образом, нам нужно сужать прямоугольник со стороны меньшей из высот, чтобы увеличить минимальную высоту «аквариума». На каждой итерации считаем площадь нового прямоугольника и сравниваем с максимумом. В случае, если и левая и правая сторона «аквариума» одинаковы — «сужаем» окно с обоих направлений.

Оценка сложности #

По времени

На каждой итерации мы двигаем либо правую, либо левую границу окна. Таким образом, суммарно мы подвинем границу O(n - 1) раз. Это единственная переменная величина. Таким образом, алгоритм имеет линейный порядок роста O(n).

По памяти

Мы никак не преобразуем входящие данные и не храним промежуточные результаты (как в случае с брутфорсом). Сложность по памяти константная — O(1).