Лучшее время для покупки и продажи акций II
Описание задачи #
Дан целочисленный массив цен prices, где prices[i] — цена акции на i-й день.
Каждый день вы можете принять решение о покупке и/или продаже акции. Вы можете одновременно владеть не более одной акцией.
Найдите и верните максимальную прибыль, которую вы можете получить.
Ограничения #
- В массиве может быть от 1 до 3 * 104 элементов
- В качестве значений могут быть числа в диапазоне от 0 до 104
Примеры #
-
Входные данные:
[7,1,5,3,6,4]Ответ:
7Покупайте в день 2 (цена = 1) и продавайте в день 3 (цена = 5), прибыль равна
5 - 1 = 4.Затем купите в день 4 (цена = 3) и продайте в день 5 (цена = 6), прибыль равна
6 - 3 = 3.Общая прибыль равна
4 + 3 = 7. -
Входные данные:
[1,2,3,4,5]Ответ:
4Покупайте в день 1 (цена = 1) и продавайте в день 5 (цена = 5)
Прибыль равна
5 - 1 = 4. -
Входные данные:
[7,6,4,3,1]Ответ:
0Невозможно получить положительную прибыль, поэтому мы никогда не покупаем акции.
Прибыль равна
0.
Решение через локальные минимумы и максимумы #
Для получения максимальной прибыли при торговле акциями нам необходимо покупать их по самой низкой цене и продавать по самой высокой. Это означает, что покупки нужно делать в локальных минимумах, а продажу в локальных максимумах.
Возьмем для примера следующий массив цен в долларах [20, 10, 15, 5, 10, 20, 10] и представим его в виде графика.
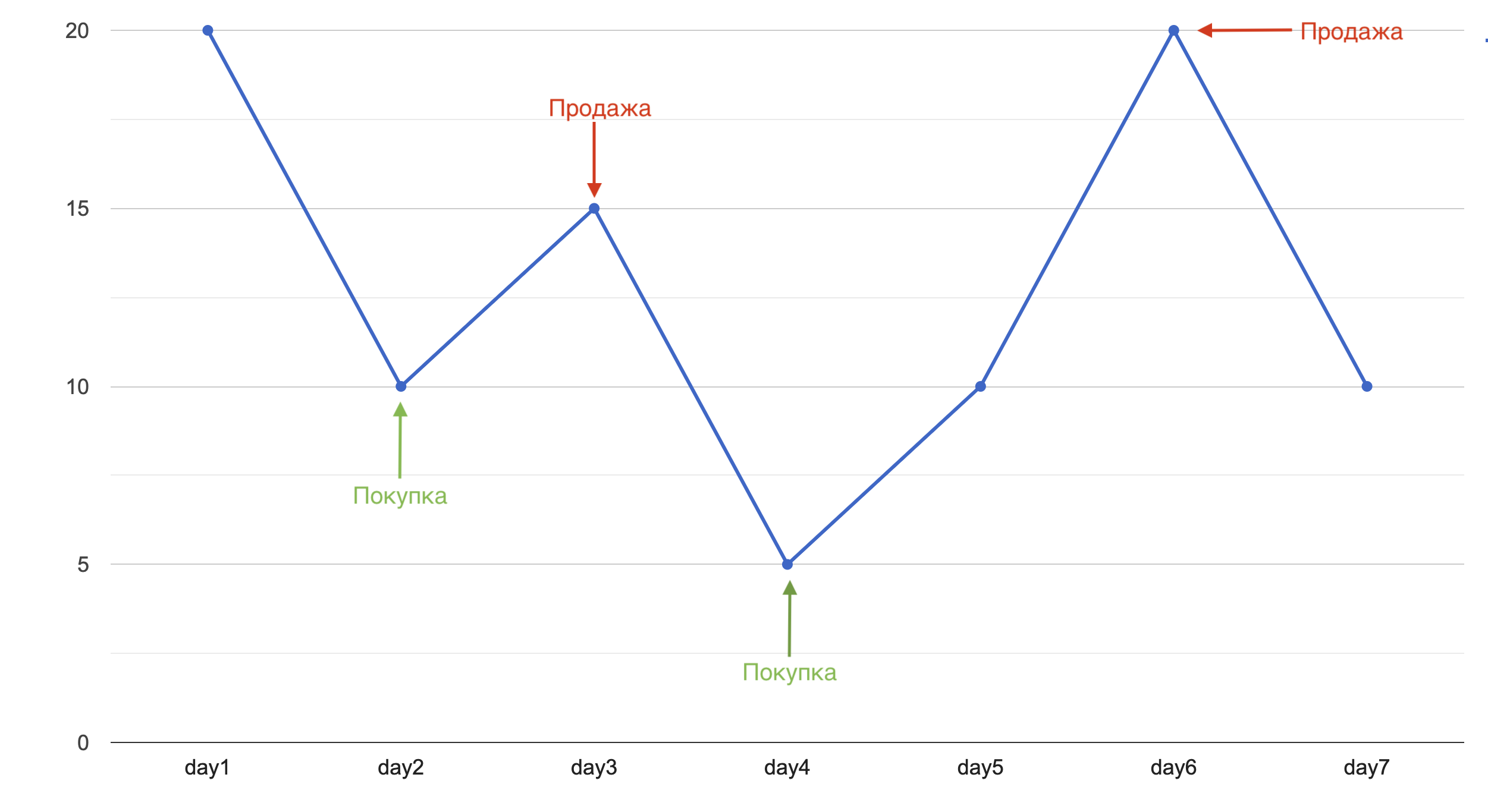
Теперь на графике хорошо видно, что нам нужно сделать две покупки и две продажи:
- купить акцию на второй день за 10 и продать на третий день за 15
- купить акцию на четвертый день за 5 и продать на шестой день за 20
В итоге мы сможем получить максимальную прибыль и заработать $20.
Таким образом решение задачи сводится к тому, что нужно проходить весь массив и искать в нем локальные минимумы и локальные максимумы. Как только мы встречаем минимум, мы запоминаем цену в этот день. Как только встречаем максимум, мы вычисляем разницу между последним минимумом и максимальной ценой и прибавляем ее к нашему общему заработку.
-
package main func maxProfitMinMax(prices []int) int { res := 0 min := prices[0] max := prices[0] for i := 1; i < len(prices); i++ { if prices[i] > max { max = prices[i] } else { res += max - min min = prices[i] max = prices[i] } } res += max - min return res } -
export const maxProfitMinMax = (prices: number[]): number => { let res = 0 let min = prices[0] let max = prices[0] for (let i = 1; i < prices.length; i++) { if (prices[i] > max) { max = prices[i] } else { res += max - min min = prices[i] max = prices[i] } } res += max - min return res }
Оценка сложности #
n - количество элементов в массиве
По времени
Сложность по времени линейная — O(n), так как мы итерируемся по всем элементам массива.
По памяти
Сложность по памяти константная — O(1), так как мы не создаем дополнительных переменных.
Решение через восходящие тренды #
Если внимательно посмотреть на график, то можно заметить, что максимальная возможная прибыль складывается из сумм разниц стоимости акции между днями на восходящих трендах.
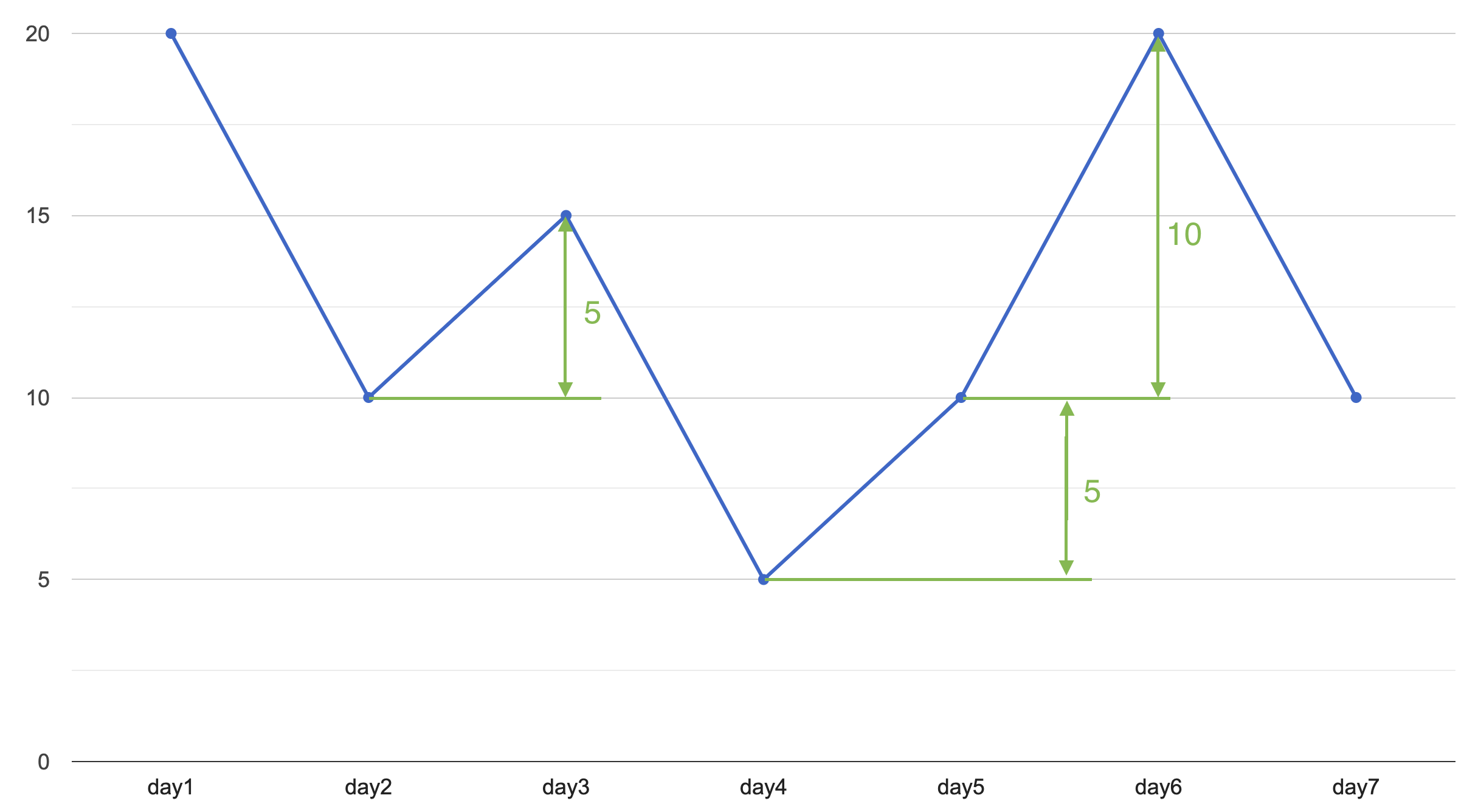
Это значит, что мы можем сильно упростить решение и не запоминать локальные минимумы и максимумы. Нам достаточно найти все возрастающие отрезки на графике и просуммировать разницу между ценой акции в эти дни.
-
package main func maxProfitTrends(prices []int) int { res := 0 for i := 0; i < len(prices)-1; i++ { if prices[i] < prices[i+1] { res += prices[i+1] - prices[i] } } return res } -
export const maxProfitTrends = (prices: number[]): number => { let res = 0 for (let i = 0; i < prices.length - 1; i++) { if (prices[i] < prices[i + 1]) { res += prices[i + 1] - prices[i] } } return res }
Оценка сложности #
n - количество элементов в массиве
По времени
Сложность по времени линейная — O(n), так как мы итерируемся по всем элементам массива.
По памяти
Сложность по памяти константная — O(1), так как мы не создаем дополнительных переменных.
